笛卡尔心形线
[toc]
说明
- 写这篇文章是因为看到一篇关于笛卡尔爱心方程的文章。给出这样一个公式 r=a(1-cosθ) ,这是笛卡尔心形线的极坐标方程,这个方程里面的确有一个浪漫又悲情的爱情故事,感兴趣的朋友可以点这里看看,而至于这个故事是真是假,这并不重要。
- 但是很多文章的配图和方程所代表的图形完全不一致!!!
- 而这篇文章的目的是要用Python编程的方式,画出笛卡尔心形线。
- 其实这么经典的公式,网上已经有很多人通过不同的方式实现过了。
- 不得不佩服网友们,有 Java 实现的,有 C# 实现的,也有 canvas 实现的,还能用 ECharts 画 ,可以学习学习。
心形线
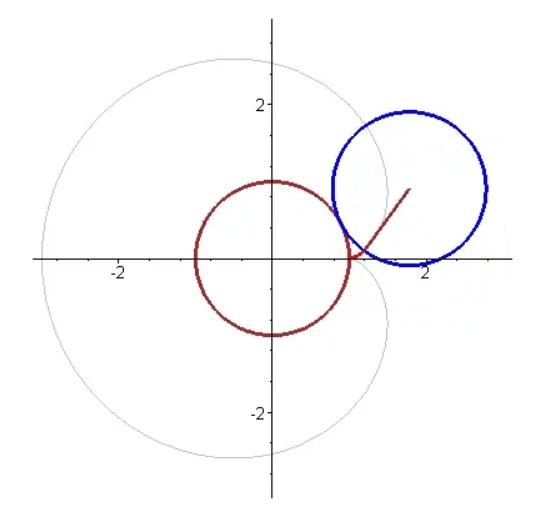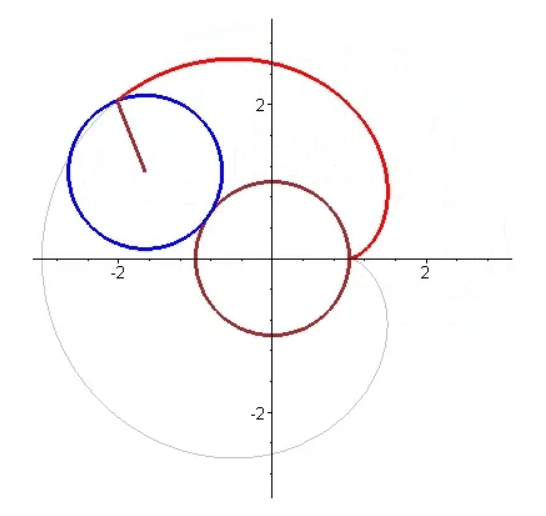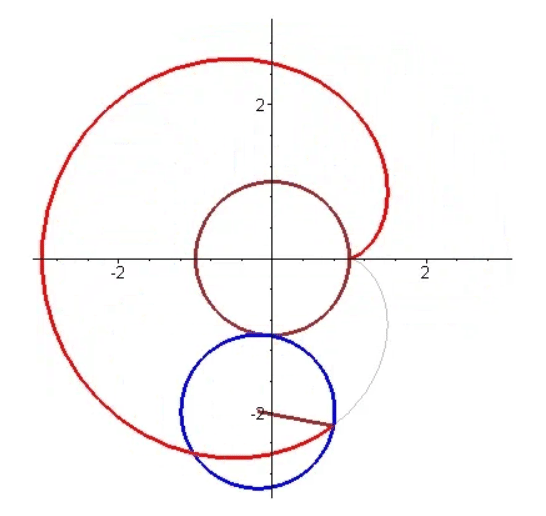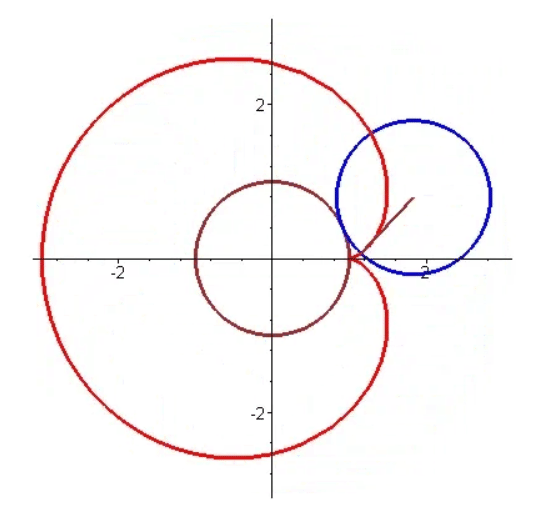
- 心形线,是一个圆上的固定一点在它绕着与其相切且半径相同的另外一个圆周滚动时所形成的轨迹,因其形状像心形而得名。
思路
根据方程表达式得到所有点的坐标,然后把每个点连接起来,然后填充,最后就行成一个心形了。
- r = a(1-cosθ)
- 首先需要将极坐标系转为笛卡尔坐标系
- 其中a的值不影响形状,方便计算,直接令a=1
- 得到:r = 1 - cosθ,r表示点到原点的距离
- 根据三角函数推出:x = r * sinθ、y = r * cosθ,带入r = 1 - cosθ
- 得出:x = (1 - cosθ) * sinθ、y = (1 - cosθ) * cosθ
- 其中θ的取值范围可以是 [0,2π] (刚好覆盖一周即可)
代码
# 将上述公式转为代码形式:
x = a * (1 - cos(t)) * sin(t)
y = a * (1 - cos(t)) * cos(t)
- x,y 分别表示一个点的 x 坐标 和 y 坐标,
- a:是一个常数,用来控制心形的大小,此处为1
- t :代表 弧度
- t 的取值范围:-pi<=t<=pi 或 0<=t<=2*pi
import numpy as np
import matplotlib.pyplot as plt
# 生成100个均匀分布的数在 [0, 2*pi] 区间内
t = np.linspace(0, 2*np.pi, 100)# t 现在包含了在 [0, 2*pi] 区间内均匀分布的100个数
x = [(1 - np.cos(i)) * np.sin(i) for i in t] # 计算x坐标的值
y = [(1 - np.cos(i)) * np.cos(i) for i in t] # 计算y坐标的值
plt.fill(x, y, 'r') # 绘制
plt.show()
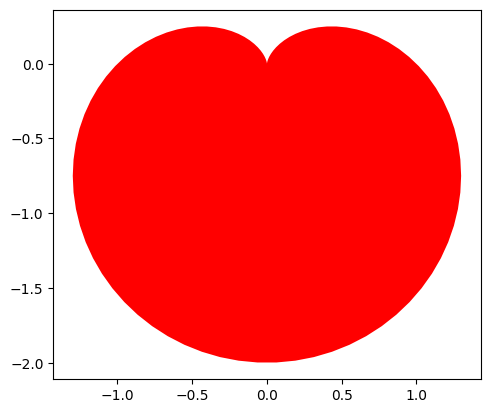
爱心形❤
- 可能你会觉得这样的心形并不好看。看看这个参数方程吧!
1 2
x=16 * sin(t) ** 3 y=13 * cos(t) - 5 * cos(2 * t) - 2 * cos(3 * t) - cos(4 * t)
根据这个参数方程,用上面说的平面直角坐标系的画法,把代码里的方程换一下,就可以画出这样的心形。
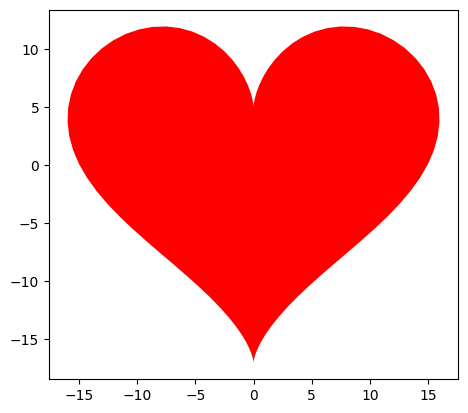
代码
import numpy as np
import matplotlib.pyplot as plt
# 生成100个均匀分布的数在 [0, 2*pi] 区间内
t = np.linspace(0, 2*np.pi, 100)# t 现在包含了在 [0, 2*pi] 区间内均匀分布的100个数
x = [16 * np.sin(i) ** 3 for i in t] # 计算x坐标的值
y = [13 * np.cos(i) - 5 * np.cos(2 * i) - 2 * np.cos(3 * i) - np.cos(4 * i) for i in t] # 计算y坐标的值
plt.fill(x, y, 'r') # 绘制
plt.show()
总结
这篇文章主要是说用笛卡尔心形线方程画心形,但是想要画出心形的方式绝对是多种多样的,单纯的用CSS也可以,复杂点用贝塞尔曲线也能画出来,大家不妨去试试,说不定又有什么新发现呢。
END